
return to the main page "Calculus II for Management"
return to the section "Vectors & Matrices"
Worked-Out Exercises: Linear Systems of Equations
The following set of exercises is given together with hints, solutions, and solution paths. They are designed such that
you can first try to solve them and in case you need help, please, open the "hints" section. For checking your
answer, please, open the "solution" section and for getting more details or checking your way of solving the
exercise, please, open the "solution path" section.
|
|
|
Exercise 1: Hagar the Horrible and gold distribution |
| |
After returning home from successful plundering Hagar the Horrible remunerates his wild horde of
vikings with gold coins (Goldstücke).
Though not every branch of service gets the same amount as we can see from his accounting list below:
- There are only 3 branches of service: ax fighter (\(A\)), sword fighter (\(S\)), and lance fighter (\(L\)).
- Each member of a branch of service gets the same amount of gold coins.
- Unfortunately, the third rule got lost over the centuries.
a) [Finding the 3rd Rule] Set-up a suitable system of linear equations to obtain the third rule
and to determine how the remuneration depends on the branch of service exactly.

b) [But Hagar is the Boss] Since decades historians debate about the actual money Hagar has taken.
Some think that he pays himself always double the amount that the others from the same branch of service get.
- How would the calculation look subject to these conditions?
- Why can this assumption not be true just like that?
- Change the total remuneration in the third line such that the contradiction vanishes,
and compute then the income of each member of a branch of service.
|
|
 Hint Hint
(please, click on the "+" sign to read more)
a) Count the number of warrior types on the image, sum them up and determine how much gold they get combined.
b) Hagar is the one with big dress and orange nose looking prideful :)
|
|
 Solution Solution
(please, click on the "+" sign to read more)
a) \(A = 1\), \(S = 3\), \(B = 4\).
b) \(\mathbb{L} = {(5 - L, 2, L) \in \mathbb{R}^3 : \mathbb{L} \in \mathbb{R}}\)
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
a) We have
$$
\begin{array}{c c c c c c c}
A & + & 2 S & + & L & = & 11 \\
A & + & S & + & 2 L & = & 12 \\
2A & + & S & + & L & = & 9
\end{array}
$$
such that the augmented matrix reads as
$$
\left( \begin{array}{ c c c | c }
1 & 2 & 1 & 11 \\
1 & 1 & 2 & 12 \\
2 & 1 & 1 & 9
\end{array} \right)
$$
Gaussian elimination:
$$
\begin{array}{c l}
%
\left( \begin{array}{ c c c | c}
1 & 2 & 1 & 11 \\
1 & 1 & 2 & 12 \\
2 & 1 & 1 & 9
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\text{$|$ $(II) - (I)$}\\
\text{$|$ $(III) - 2 \cdot (I)$}\\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 2 & 1 & 11 \\
0 & -1 & 1 & 1 \\
0 & -3 & -1 & -13
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\phantom{u} \\
\text{$|$ $- 1 \times$}\\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 2 & 1 & 11 \\
0 & -1 & 1 & 1 \\
0 & 3 & 1 & 13
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\phantom{u} \\
\phantom{u} \\
\end{array}
%
\end{array}
$$
$$
\begin{array}{c l}
%
\left( \begin{array}{ c c c | c}
1 & 2 & 1 & 11 \\
0 & -1 & 1 & 1 \\
0 & 3 & 1 & 13
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\phantom{u} \\
\text{$|$ $(III) + 3 \cdot (II)$}\\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 2 & 1 & 11 \\
0 & -1 & 1 & 1 \\
0 & 0 & 4 & 16
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\text{$|$ $-1 \times$} \\
\text{$|$ $\tfrac{1}{4} \times$}\\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 2 & 1 & 11 \\
0 & 1 & -1 & -1 \\
0 & 0 & 1 & 4
\end{array} \right)
\\[2mm]
\Downarrow
%
\end{array}
$$
$$
\begin{array}{c l}
%
\left( \begin{array}{ c c c | c}
1 & 2 & 1 & 11 \\
0 & 1 & -1 & -1 \\
0 & 0 & 1 & 4
\end{array} \right)
& \begin{array}{l}
\text{$|$ $(I) - (III)$}\\
\text{$|$ $(II) + (III)$}\\
\phantom{u} \\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 2 & 0 & 7 \\
0 & 1 & 0 & 3 \\
0 & 0 & 1 & 4
\end{array} \right)
& \begin{array}{l}
\text{$|$ $(I) - 2 (II)$}\\
\phantom{u} \\
\phantom{u} \\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
\left( \begin{array}{ c c c | c}
1 & 0 & 0 & 1 \\
0 & 1 & 0 & 3 \\
0 & 0 & 1 & 4
\end{array} \right)
%
\end{array}
$$
Finally,
\begin{eqnarray*}
A & = & 1 \\
S & = & 3 \\
L & = & 4 \\
\end{eqnarray*}
b) When we inspect the linear system of equation that results form the 'Hagar is the boss' assumption, we have
$$
\begin{array}{c c c c c c c}
A & + & 3 S & + & L & = & 11 \\
2A & + & S & + & 2 L & = & 12 \\
2A & + & S & + & 2 L & = & 9
\end{array}
$$
One way to resolve the situation is to instead consider the underdetermined system
$$
\begin{array}{c c c c c c c}
A & + & 3 S & + & L & = & 11 \\
2A & + & S & + & 2 L & = & 12
\end{array}
$$
Hence, we have the situation of infintely many solutions (which is the case when we have an underdetermined system anyway).
Let us use \(L\) as the free variable, then we get
$$
A \, \, = \, \, 5 - L \quad \text{and} \quad S \, \, = \, \, 2
$$
and thus
$$
\mathbb{L} \, \, = \, \, \left\{ (5-L , 2, L) \in \mathbb{R}^3 \, : \, L \, \in \, \mathbb{R} \right\}
$$
which is the equation of a line in 3D space.
$$
\begin{array}{c l}
%
\left( \begin{array}{ c c c | c}
1 & 3 & 1 & 11 \\
2 & 1 & 2 & 12
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\text{$|$ $(II) - 2 \cdot (I)$}\\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 3 & 1 & 11 \\
0 & -5 & 0 & -10
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\text{$|$ $-\tfrac{1}{5} \times$} \\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 3 & 1 & 11 \\
0 & 1 & 0 & 2
\end{array} \right)
& \begin{array}{l}
\text{$|$ $(I) - 3 \cdot (II)$} \\
\phantom{u} \\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 0 & 1 & 5 \\
0 & 1 & 0 & 2
\end{array} \right)
\end{array}
$$
|
|
Exercise 2: Conditions for one, zero and infinite amount of solutions for a system |
| |
Depending on the choice of the real constants \( a \) and \( b \) give the feasible
solution set of the following system of two equations in two unknowns. I.e., determine \( a, b \in \mathbb{R} \)
such that this system may have none, exactly one, or infinitely many solutions.
- \(x + by = -1\) and \(ax + 2y = 5\).
- \(x - 2y = 1\) and \(ax + by = 5\)
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Bring the systems of equations first to upper echelon form (for the augmented matrix) and then interpret the result: no solution,
exactly one, or infinitely many solutions. In particular, we have no solution when \(0 \cdot x = a\) where \(a\) is non-zero, infinitely
many solutions when \(0 \cdot x = 0 \) and one solution when \(a \cdot x = b\) where \(a\) and \(b\) are not \(0\).
|
|
 Solution Solution
(please, click on the "+" sign to read more)
a) No solution: \(a\) ≠ \(-5\) & \(ab = 2\), ∞ many solutions: \(a = 5\) & \(ab = 2\), Unique solution: \(ab\) ≠ \(2\)
b) No solution: \(a\) ≠ \(-5\) & \(b = 2a\), ∞ many solutions: \(a = 5\) & \(b = -2a\), Unique solution: \(b\) ≠ \(-2a\)
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
a) For \(x + by = -1\) and \(ax + 2y = 5\) we have with \((II) - a \cdot (I)\)
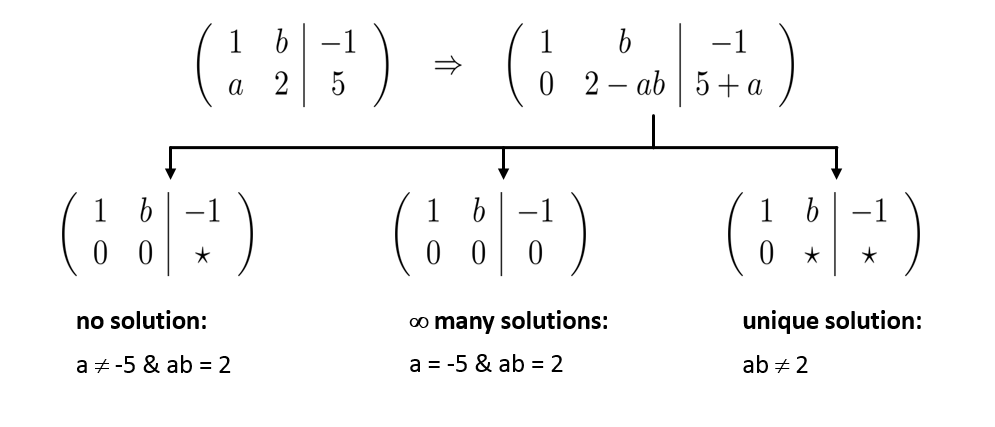
b) For \(x - 2y = 1\) and \(ax + by = 5\) we have with \((II) - a \cdot (I)\)
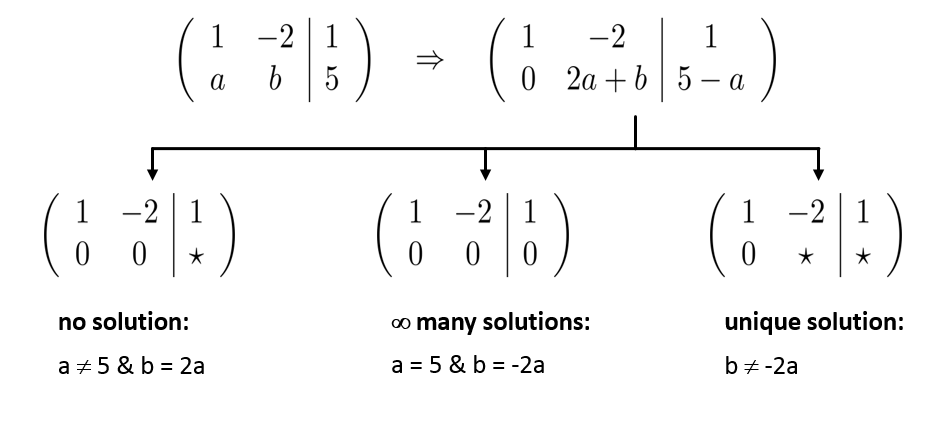
|
|
Exercise 3: Solving linear systems |
| |
Determine the solution set of the following linear systems of equations by bringing them
first to upper echelon form (for the augmented matrix) and then perform a back-substitution to gain the results (make sure you
write down the elementary operations you use). Finally, interpret the result geometrically:
- \(x_1 + 5 x_2 = 7\) and \(-2x_1 - 7x_2 = -5\)
- \(x_1 + x_2 - x_3 = 1\), \(2x_1 + x_2 - x_3 = 6\) and \(3x_1 + 7x_2 - 7x_3 = -13\)
|
|
 Hint Hint
(please, click on the "+" sign to read more)
Bring the systems of equations first to upper echelon form (for the augmented matrix) and then perform a back-substitution
to gain the results (make sure you write down the elementary operations you use). Finally, interpret the result geometrically.
|
|
 Solution Solution
(please, click on the "+" sign to read more)
a) \((-8, 3)\)
b) \(\mathbb{L} = {(5 , s-4, s) \in \mathbb{R}^3 : s \in \mathbb{R}}\)
|
|
 Solution Path Solution Path
(please, click on the "+" sign to read more)
a) We have $$
\begin{array}{c l}
%
\left( \begin{array}{ c c | c}
1 & 5 & 7 \\
-2 & -7 & -5
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\text{$|$ $(II) + 2 \cdot (I)$}\\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c | c}
1 & 5 & 7 \\
0 & 3 & 9
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\text{$|$ $\frac{1}{3} \times$} \\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c | c}
1 & 5 & 7 \\
0 & 1 & 3
\end{array} \right)
& \begin{array}{l}
\text{$|$ $(I) - 5 \cdot (II)$} \\
\phantom{u} \\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c | c}
1 & 0 & -8 \\
0 & 1 & 3
\end{array} \right)
\end{array}
$$
Hence, we have \((x_1,x_2) = (-8,3)\) as a candidate for the solution.
We validate this candidate via matrix-column multiplication:
\begin{eqnarray*}
\begin{pmatrix}
1 & 5\\ -2 & -7
\end{pmatrix}
\begin{pmatrix}
-8 \\ 3
\end{pmatrix}
& = &
\begin{pmatrix}
1 \cdot (-8) + 5 \cdot 3 \\
-2 \cdot (-8) + (-7) \cdot 3
\end{pmatrix} \\
& = &
\begin{pmatrix}
-8 + 15 \\
16 -21
\end{pmatrix} \\
& = &
\begin{pmatrix}
7 \\ -5
\end{pmatrix}
\end{eqnarray*}
Thus, \((-8,3)\) is indeed the unique solution.
b) We have $$
\begin{array}{c l}
%
\left( \begin{array}{ c c c | c}
1 & 1 & -1 & 1 \\
2 & 1 & -1 & 6 \\
3 & 7 & -7 & -13
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\text{$|$ $(II) - 2 \cdot (I)$}\\
\text{$|$ $(III) - 3 \cdot (I)$}\\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 1 & -1 & 1 \\
0 & -1 & 1 & 4 \\
0 & 4 & -4 & -16
\end{array} \right)
& \begin{array}{l}
\phantom{u} \\
\phantom{u} \\
\text{$|$ $(III) + 4 \cdot (II)$} \\
\end{array}
\\[2mm]
\Downarrow \\[2mm]
%
\left( \begin{array}{ c c c | c}
1 & 1 & -1 & 1 \\
0 & -1 & 1 & 4 \\
0 & 0 & 0 & 0
\end{array} \right)
\end{array}
$$
Hence, we have the situation of infintely many solutions.
Let us use \(x_3 = s\) as the free variable, then we get
$$
x_1 \, \, = \, \, 5 \quad \text{and} \quad x_2 \, \, = \, \, s-4
$$
and thus
$$
\mathbb{L} \, \, = \, \, \left\{ (5 , s-4, s) \in \mathbb{R}^3 \, : \, s \, \in \, \mathbb{R} \right\}
$$
which is the equation of a line in 3D space.
Finally, we perform the matrix-column multiplication to verify the solution:
\begin{eqnarray*}
\begin{pmatrix}
1 & 1 & -1 \\
2 & 1 & -1 \\
3 & 7 & -7
\end{pmatrix}
\begin{pmatrix}
5 \\ s-4 \\ s
\end{pmatrix}
& = &
\begin{pmatrix}
1 \cdot 5 + 1 \cdot (s-4) + (-1) \cdot s \\
2 \cdot 5 + 1 \cdot (s-4) + (-1) \cdot s \\
3 \cdot 5 + 7 \cdot (s-4) + (-7) \cdot s
\end{pmatrix}\\[2mm]
& = &
\begin{pmatrix}
5 + s - 4 - s \\
10 + s - 4 - s \\
15 + 7s - 28 - 7s
\end{pmatrix} \\[2mm]
& = &
\begin{pmatrix}
1 \\
6 \\
-13
\end{pmatrix}
\end{eqnarray*}
|
|
|
|
Copyright Kutaisi International University — All Rights Reserved — Last Modified: 12/ 10/ 2022
|
|
|

